The ticket prices for a concert are shown in the following table.

• A total of $600$ tickets were sold.
• The total amount of money from ticket sales was $\$7816$.
• There were twice as many adult tickets sold as child tickets.

Let the number of adult tickets sold be $x$, the number of child tickets sold be $y$, and the number of student tickets sold be $z$.

The strength of earthquakes is measured on the Richter magnitude scale, with values typically between $0$ and $8$ where $8$ is the most severe.

The Gutenberg–Richter equation gives the average number of earthquakes per year, $N$, which have a magnitude of at least $M$. For a particular region the equation is

${\log }_{10} N=a-M$, for some $a\in \mathrm{ℝ}$.

This region has an average of $100$ earthquakes per year with a magnitude of at least $3$.

The equation for this region can also be written as $N=\frac{b}{{10}^M}$.

The expected length of time, in years, between earthquakes with a magnitude of at least $M$ is $\frac{1}{N}$.

Within this region the most severe earthquake recorded had a magnitude of $7.2$.

Let the function $h\left(x\right)$ represent the height in centimetres of a cylindrical tin can with diameter $x\text{\hspace{0.05em}cm}$.

$h\left(x\right)=\frac{640}{x^2}+0.5$ for $4\le x\le 14$.

The function $h^{-1}$ is the inverse function of $h$.

Charlie and Daniella each began a fitness programme. On day one, they both ran $500 \text{m}$. On each subsequent day, Charlie ran $100 \text{m}$ more than the previous day whereas Daniella increased her distance by $2\%$ of the distance ran on the previous day.

Calculate how far

Consider the function $f\left(x\right)=a{x}^2+bx+c$. The graph of $y=f\left(x\right)$ is shown in the diagram. The vertex of the graph has coordinates $(0.5, -12.5)$. The graph intersects the $x$-axis at two points, $(-2, 0)$ and $(p, 0)$.

A factory produces engraved gold disks. The cost $C$ of the disks is directly proportional to the cube of the radius $r$ of the disk.

A disk with a radius of $0.8$cm costs $375$US dollars (USD).

The height of a baseball after it is hit by a bat is modelled by the function

$h\left(t\right)=-4.8t^2+21t+1.2$

where $h\left(t\right)$ is the height in metres above the ground and $t$ is the time in seconds after the ball was hit.

Let $f\left(x\right)=x^2-<!--\; -\; -->4x-<!--\; -\; -->5$. The following diagram shows part of the graph of $f$.

The function can be written in the form $f\left(x\right)={\left(x-<!--\; -\; -->h\right)}^2+k$.

Sejah placed a baking tin, that contained cake mix, in a preheated oven in order to bake a cake. The temperature in the centre of the cake mix, $T$, in degrees Celsius (°C) is given by

$$T(t)=150-<!--\; -\; -->a\times <!--\; \times \; -->(1.1{)}^{-<!--\; -\; -->t}$$

where $t$ is the time, in minutes, since the baking tin was placed in the oven. The graph of $T$ is shown in the following diagram.

The temperature in the centre of the cake mix was 18 °C when placed in the oven.

The baking tin is removed from the oven 15 minutes after the temperature in the centre of the cake mix has reached 130 °C.

The following diagram shows part of the graph of $f$ with $x$-intercept (5, 0) and $y$-intercept (0, 8).

A quadratic function $f$ is given by $f(x)=a{x}^2+bx+c$. The points $(0,5)$ and $(-<!--\; -\; -->4,5)$ lie on the graph of $y=f(x)$.

The $y$-coordinate of the minimum of the graph is 3.

The size of a computer screen is the length of its diagonal. Zuzana buys a rectangular computer screen with a size of 68 cm, a height of $y$ cm and a width of $x$ cm, as shown in the diagram.

The ratio between the height and the width of the screen is 3:4.

Let f(x) = ax² − 4x − c. A horizontal line, L , intersects the graph of f at x = −1 and x = 3.

Jashanti is saving money to buy a car. The price of the car, in US Dollars (USD), can be modelled by the equation

$$P=8500(0.95{)}^t.$$

Jashanti’s savings, in USD, can be modelled by the equation

$$S=400t+2000.$$

In both equations $t$ is the time in months since Jashanti started saving for the car.

Jashanti does not want to wait too long and wants to buy the car two months after she started saving. She decides to ask her parents for the extra money that she needs.

Olava’s Pizza Company supplies and delivers large cheese pizzas.

The total cost to the customer, $C$, in Papua New Guinean Kina ($\text{PGK}$), is modelled by the function

$C\left(n\right)=34.50n+8.50 , n\ge 2 , n\in \mathrm{\mathbb{Z}},$

where $n$, is the number of large cheese pizzas ordered. This total cost includes a fixed cost for delivery.

The price of gas at Leon’s gas station is $\$1.50$ per litre. If a customer buys a minimum of $10$ litres, a discount of $\$5$ is applied.

This can be modelled by the following function, $L$, which gives the total cost when buying a minimum of $10$ litres at Leon’s gas station.

$L\left(x\right)=1.50x-5, x\ge 10$

where $x$ is the number of litres of gas that a customer buys.

The size of the population $\left(P\right)$ of migrating birds in a particular town can be approximately modelled by the equation $P=a \sin \left(bt\right)+c, a, b, c\in {\mathrm{ℝ}}^{+}$, where $t$ is measured in months from the time of the initial measurements.

In a $12$ month period the maximum population is $2600$ and occurs when $t=3$ and the minimum population is $800$ and occurs when $t=9$.

This information is shown on the graph below.

Irina uses a set of coordinate axes to draw her design of a window. The base of the window is on the $x$-axis, the upper part of the window is in the form of a quadratic curve and the sides are vertical lines, as shown on the diagram. The curve has end points $(0, 10)$ and $(8, 10)$ and its vertex is $(4, 12)$. Distances are measured in centimetres.

The quadratic curve can be expressed in the form $y=a{x}^2+bx+c$ for $0\le x\le 8$.

Consider the curve y = 5x³ − 3x.

The curve has a tangent at the point P(−1, −2).

Consider the function $f\left(x\right)=\frac{x^4}{4}$.

Elvis Presley is an extremely popular singer. Although he passed away in $1977$, many of his fans continue to pay tribute by dressing like Elvis and singing his songs.

The number of Elvis impersonators, $N\left(t\right)$, can be modelled by the function

$N\left(t\right)=170\times 1.{31}^t,$

where $t$, is the number of years since $1977$.

The diagram shows the graph of the quadratic function $f\left(x\right)=a{x}^2+bx+c$ , with vertex $\left(-2, 10\right)$.

The equation $f\left(x\right)=k$ has two solutions. One of these solutions is $x=2$.

If a shark is spotted near to Brighton beach, a lifeguard will activate a siren to warn swimmers.

The sound intensity, $I$, of the siren varies inversely with the square of the distance, $d$, from the siren, where $d>0$.

It is known that at a distance of $1.5$ metres from the siren, the sound intensity is $4$ watts per square metre (${\text{W\hspace{0.05em}m}}^{-2}$).

A function $f$ is given by $f(x)=4x^3+\frac{3}{x^2}-<!--\; -\; -->3,x\ne <!--\; \ne \; -->0$.

Maria owns a cheese factory. The amount of cheese, in kilograms, Maria sells in one week, $Q$, is given by

$Q=882-<!--\; -\; -->45p$,

where $p$ is the price of a kilogram of cheese in euros (EUR).

Maria earns $(p-<!--\; -\; -->6.80)\text{ EUR}$ for each kilogram of cheese sold.

To calculate her weekly profit $W$, in EUR, Maria multiplies the amount of cheese she sells by the amount she earns per kilogram.

The following function models the growth of a bacteria population in an experiment,

P(t) = A × 2^t,  t ≥ 0

where A is a constant and t is the time, in hours, since the experiment began.

Four hours after the experiment began, the bacteria population is 6400.

The cross-section of an arched entrance into the ballroom of a hotel is in the shape of a parabola. This cross-section can be modelled by part of the graph $y=-1.6x^2+4.48x$, where $y$ is the height of the archway, in metres, at a horizontal distance, $x$ metres, from the point $\text{O}$, in the bottom corner of the archway.

To prepare for an event, a square-based crate that is $1.6 \text{m}$ wide and $2.0 \text{m}$ high is to be moved through the archway into the ballroom. The crate must remain upright while it is being moved.

Little Green island originally had no turtles. After 55 turtles were introduced to the island, their population is modelled by

$$N\left(t\right)=a\times <!--\; \times \; -->2^{-<!--\; -\; -->t}+10\text{,}t⩾<!--\; ⩾\; -->0\text{,}$$

where $a$ is a constant and $t$ is the time in years since the turtles were introduced.

A factory produces shirts. The cost, C, in Fijian dollars (FJD), of producing x shirts can be modelled by

C(x) = (x − 75)² + 100.

The cost of production should not exceed 500 FJD. To do this the factory needs to produce at least 55 shirts and at most s shirts.

The graph below shows the average savings, $S$ thousand dollars, of a group of university graduates as a function of $t$, the number of years after graduating from university.

The equation of the model can be expressed in the form $S=a{t}^3+b{t}^2+ct+d$, where $a, b, c$ and $d$ are real constants.

The graph of the model must pass through the following four points.

A negative value of $S$ indicates that a graduate is expected to be in debt.

Let $f(x)=x^2-<!--\; -\; -->4x+5$.

The function can also be expressed in the form $f(x)=(x-<!--\; -\; -->h{)}^2+k$.

The function $f$ is of the form $f(x)=ax+b+\frac{c}{x}$, where $a$ , $b$ and $c$ are positive integers.

Part of the graph of $y=f(x)$ is shown on the axes below. The graph of the function has its local maximum at $(-<!--\; -\; -->2,-<!--\; -\; -->2)$ and its local minimum at $(2,6)$.

Professor Wei observed that students have difficulty remembering the information presented in his lectures.

He modelled the percentage of information retained, $R$, by the function $R\left(t\right)=100{\text{e}}^{-pt}$, $t\ge 0$, where $t$ is the number of days after the lecture.

He found that $1$ day after a lecture, students had forgotten $50\%$ of the information presented.

Based on his model, Professor Wei believes that his students will always retain some information from his lecture.

Professor Vinculum investigated the migration season of the Bulbul bird from their natural wetlands to a warmer climate.

He found that during the migration season their population, $P$ could be modelled by $P=1350+400{\left(1.25\right)}^{-<!--\; -\; -->t}$, $t$ ≥ 0 , where $t$ is the number of days since the start of the migration season.

The amount, in milligrams, of a medicinal drug in the body $t$ hours after it was injected is given by $D\left(t\right)=23(0.85{)}^t, t\ge 0$. Before this injection, the amount of the drug in the body was zero.

Write down

In an experiment, a number of fruit flies are placed in a container. The population of fruit flies, P , increases and can be modelled by the function

$$P\left(t\right)=12\times <!--\; \times \; -->3^{0.498t},t⩾<!--\; ⩾\; -->0,$$

where t is the number of days since the fruit flies were placed in the container.

The graph of the quadratic function $f(x)=c+bx-<!--\; -\; -->x^2$ intersects the $x$-axis at the point $\text{A}(-<!--\; -\; -->1,0)$ and has its vertex at the point $\text{B}(3,16)$.

The amount of yeast, g grams, in a sugar solution can be modelled by the function,

g(t) = 10 − k(c^−t) for t ≥ 0

where t is the time in minutes.

The graph of g(t) is shown.

The initial amount of yeast in this solution is 2 grams.

The amount of yeast in this solution after 3 minutes is 9 grams.

Consider the quadratic function $f\left(x\right)=a{x}^2+bx+22$.

The equation of the line of symmetry of the graph $y=f\left(x\right)\text{ is }x=1.75$.

The graph intersects the x-axis at the point (−2 , 0).

A function is defined by $f\left(x\right)=2-\frac{12}{x+5}$ for $-7\le x\le 7, x\ne -5$.

The following diagram shows the graph of a function $f$, for −4 ≤ x ≤ 2.

Consider the graph of the function $f\left(x\right)=x+\frac{12}{x^2}, x\ne 0$.

Consider the function $f\left(x\right)=x^2-\frac{3}{x}, x\ne 0$.

Line $L$ is a tangent to $f\left(x\right)$ at the point $(1, -2)$.

Dilara is designing a kite $\text{ABCD}$ on a set of coordinate axes in which one unit represents $10 \text{cm}$.

The coordinates of $\text{A}$, $\text{B}$ and $\text{C}$ are $(2, 0), (0, 4)$ and $(4, 6)$ respectively. Point $\text{D}$ lies on the $x$-axis. $\left[\text{AC}\right]$ is perpendicular to $\left[\text{BD}\right]$. This information is shown in the following diagram.

Gabriella purchases a new car.

The car’s value in dollars, $V$, is modelled by the function

$$V(t)=12870-<!--\; -\; -->k(1.1{)}^t,t⩾<!--\; ⩾\; -->0$$

where $t$ is the number of years since the car was purchased and $k$ is a constant.

After two years, the car’s value is $9143.20.

This model is defined for $0⩽<!--\; ⩽\; -->t⩽<!--\; ⩽\; -->n$. At $n$ years the car’s value will be zero dollars.

Natasha carries out an experiment on the growth of mould. She believes that the growth can be modelled by an exponential function

$P\left(t\right)=A{\text{e}}^{kt}$,

where $P$ is the area covered by mould in ${\text{mm}}^{\text{2}}$, $t$ is the time in days since the start of the experiment and $A$ and $k$ are constants.

The area covered by mould is $112 {\text{mm}}^2$ at the start of the experiment and $360 {\text{mm}}^2$ after $5$ days.

The coordinates of point A are $(6,-<!--\; -\; -->7)$ and the coordinates of point B are $(-<!--\; -\; -->6,2)$. Point M is the midpoint of AB.

$L_1$ is the line through A and B.

The line $L_2$ is perpendicular to $L_1$ and passes through M.

The intensity level of sound, $L$ measured in decibels (dB), is a function of the sound intensity, $S$ watts per square metre (W m⁻²). The intensity level is given by the following formula.

$L=10\text{lo}{\text{g}}_{10}\left(S\times <!--\; \times \; -->{10}^{12}\right)$, $S$ ≥ 0.

The pH of a solution measures its acidity and can be determined using the formula pH $=-{\log }_{10} C$, where $C$ is the concentration of hydronium ions in the solution, measured in moles per litre. A lower pH indicates a more acidic solution.

The concentration of hydronium ions in a particular type of coffee is $1.3\times 10{}^{-5}$ moles per litre.

A different, unknown, liquid has $10$ times the concentration of hydronium ions of the coffee in part (a).

The diagram shows part of the graph of a function $y=f(x)$. The graph passes through point $\text{A}(1,3)$.

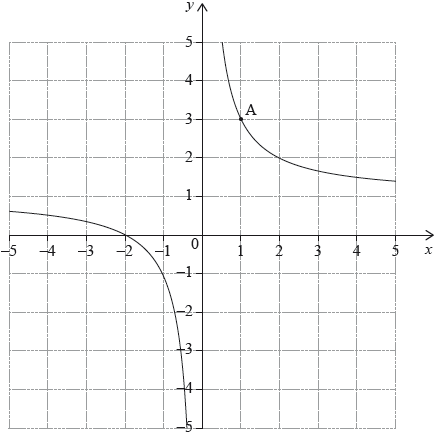
The tangent to the graph of $y=f(x)$ at A has equation $y=-<!--\; -\; -->2x+5$. Let $N$ be the normal to the graph of $y=f(x)$ at A.

Consider the straight lines L₁ and L₂. R is the point of intersection of these lines.

The equation of line L₁ is y = ax + 5.

The equation of line L₂ is y = −2x + 3.

In this question, give your answers to the nearest whole number.

Criselda travelled to Kota Kinabalu in Malaysia. At the airport, she saw the following information at the Currency Exchange counter.

This means the Currency Exchange counter would buy $\text{USD}$ from a traveller and in exchange return $\text{MYR}$ at a rate of $1 \text{USD}=4.25 \text{MYR}$. There is no commission charged.

Criselda changed $460$ $\text{SGD}$ to $\text{MYR}$.

Consider the graph of the function $f\left(x\right)=\frac{3}{x}-<!--\; -\; -->2,x\ne <!--\; \ne \; -->0$.

The following diagram shows part of the graph of $f\left(x\right)=\frac{k}{x}$, for $x>0, k>0$.

Let $\text{P}\left(p, \frac{k}{p}\right)$ be any point on the graph of $f$. Line $L_1$ is the tangent to the graph of $f$ at $\text{P}$.

Line $L_1$ intersects the $x$-axis at point $\text{A}\left(2p, 0\right)$ and the $y$-axis at point B.

M-Line is a company that prints and sells custom designs on T-shirts. For each order, they charge an initial design fee and then an additional fee for each printed T-shirt.

M-Line charges $M$ euros per order. This charge is modelled by the linear function $M\left(x\right)=5x+40$, where $x$ is the number of T-shirts in the order.

EnYear is another company that prints and sells T-shirts. The price, $N$ euros, that they charge for an order can be modelled by the linear function $N\left(x\right)=9x$, where $x$ is the number of T-shirts in the order.

Jean-Pierre jumps out of an airplane that is flying at constant altitude. Before opening his parachute, he goes through a period of freefall.

Jean-Pierre’s vertical speed during the time of freefall, $S$, in ${\text{m\hspace{0.05em}s}}^{-1}$, is modelled by the following function.

$S\left(t\right)=K-60\left(1.2^{-t}\right) , t\ge 0$

where $t$, is the number of seconds after he jumps out of the airplane, and $K$ is a constant. A sketch of Jean-Pierre’s vertical speed against time is shown below.

Jean-Pierre’s initial vertical speed is $0 {\text{m\hspace{0.05em}s}}^{-1}$.

Three towns, $\text{A}$, $\text{B}$ and $\text{C}$ are represented as coordinates on a map, where the $x$ and $y$ axes represent the distances east and north of an origin, respectively, measured in kilometres.

Town $\text{A}$ is located at $(-6, -1)$ and town $\text{B}$ is located at $(8, 6)$. A road runs along the perpendicular bisector of $\text{[AB]}$. This information is shown in the following diagram.

The graph of a quadratic function has $y$-intercept 10 and one of its $x$-intercepts is 1.

The $x$-coordinate of the vertex of the graph is 3.

The equation of the quadratic function is in the form $y=a{x}^2+bx+c$.

Line $L$ intersects the $x$-axis at point A and the $y$-axis at point B, as shown on the diagram.

The length of line segment OB is three times the length of line segment OA, where O is the origin.

Point $\text{(2, 6)}$ lies on $L$.

A potter sells $x$ vases per month.

His monthly profit in Australian dollars (AUD) can be modelled by

$$P\left(x\right)=-<!--\; -\; -->\frac{1}{5}{x}^3+7x^2-<!--\; -\; -->120\text{,}x⩾<!--\; ⩾\; -->0.$$

In this question, give all answers to two decimal places.

Karl invests 1000 US dollars (USD) in an account that pays a nominal annual interest of 3.5%, compounded quarterly. He leaves the money in the account for 5 years.

Consider a function f (x) , for −2 ≤ x ≤ 2 . The following diagram shows the graph of f.

Let $f(x)=1+{\text{e}}^{-<!--\; -\; -->x}$ and $g(x)=2x+b$, for $x\in <!--\; \in \; -->\mathbb{R}$, where $b$ is a constant.